Milankovitch cycles

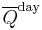Past and future Milankovitch cycles. VSOP allows prediction of past and future orbital parameters with great accuracy. ε is obliquity (axial tilt). e is eccentricity. ϖ is longitude of perihelion. esin(ϖ) is the precession index, which together with obliquity, controls the seasonal cycle of insolation. \overline{Q}^{\mathrm{day}} is the calculated daily-averaged insolation at the top of the atmosphere, on the day of the summer solstice at 65 N latitude. Benthic forams and Vostok ice core show two distinct proxies for past global sealevel and temperature, from ocean sediment and Antarctic ice respectively. Vertical gray line is current conditions, at 2 ky A.D.

Milankovitch Theory describes the collective effects of changes in the Earth's movements upon its climate, named after Serbian civil engineer and mathematician Milutin Milanković, who worked on it during First World War internment. Milanković mathematically theorised that variations in eccentricity, axial tilt, and precession of the Earth's orbit determined climatic patterns on Earth.

The Earth's axis completes one full cycle of precession approximately every 26,000 years. At the same time, the elliptical orbit rotates, more slowly, leading to a 21,000-year cycle between the seasons and the orbit. In addition, the angle between Earth's rotational axis and the normal to the plane of its orbit moves from 22.1 degrees to 24.5 degrees and back again on a 41,000-year cycle; currently, this angle is 23.44 degrees and is decreasing.

Other astronomical theories were advanced by Joseph Adhemar, James Croll and others, but verification was difficult due to the absence of reliably dated evidence and doubts as to exactly which periods were important. Not until the advent of deep-ocean cores and a seminal paper by Hays, Imbrie and Shackleton, "Variations in the Earth's Orbit: Pacemaker of the Ice Ages", in Science, 1976,[1] did the theory attain its present state.

Contents

Earth’s movements

As the Earth spins around its axis and orbits around the Sun, several quasi-periodic variations occur. Although the curves have a large number of sinusoidal components, a few components are dominant.[2] Milankovitch studied changes in the orbital eccentricity, obliquity, and precession of Earth's movements. Such changes in movement and orientation change the amount and location of solar radiation reaching the Earth. This is known as solar forcing (an example of radiative forcing). Changes near the north polar area are considered important due to the large amount of land, which reacts to such changes more quickly than the oceans do.

Orbital shape (eccentricity)

Main article: Orbital eccentricity
Circular orbit, no eccentricity.
Orbit with 0.5 eccentricity.

The Earth's orbit is an ellipse. The eccentricity is a measure of the departure of this ellipse from circularity. The shape of the Earth's orbit varies in time between being nearly circular (low eccentricity of 0.005) and being mildly elliptical (high eccentricity of 0.058) and has a mean eccentricity of 0.028. The major component of these variations occurs on a period of 413,000 years (eccentricity variation of ±0.012). A number of other terms vary between components 95,000 and 125,000 years (with a beat period 400,000 years), and loosely combine into a 100,000-year cycle (variation of −0.03 to +0.02). The present eccentricity is 0.017.

If the Earth were the only planet orbiting our Sun, the eccentricity of its orbit would not perceptibly vary even over a period of a million years. The Earth's eccentricity varies primarily due to interactions with the gravitational fields of Jupiter and Saturn. As the eccentricity of the orbit evolves, the semi-major axis of the orbital ellipse remains unchanged. From the perspective of the perturbation theory used in celestial mechanics to compute the evolution of the orbit, the semi-major axis is an adiabatic invariant. According to Kepler's third law the period of the orbit is determined by the semi-major axis. It follows that the Earth's orbital period, the length of a sidereal year, also remains unchanged as the orbit evolves. As the semi-minor axis is decreased with the eccentricity increase, the seasonal changes increase.[3] But the mean solar irradiation for the planet changes only slightly for small eccentricity, due to Kepler's second law.

The same average irradiation does not correspond to the average of corresponding temperatures (due to non-linearity of the Stefan–Boltzmann law). For an irradiation with corresponding temperature 20°C and its symmetric variation ±50% (e.g. from the seasons change[4]) we obtain asymmetric variation of corresponding temperatures with their average 16°C (i.e. deviation -4°C). And for the irradiation variation during a day (with its average corresponding also to 20°C) we obtain the average temperature (for zero thermal capacity) -113°C.

The relative increase in solar irradiation at closest approach to the Sun (perihelion) compared to the irradiation at the furthest distance (aphelion) is slightly larger than 4 times the eccentricity. For the current orbital eccentricity this amounts to a variation in incoming solar radiation of about 6.8%, while the current difference between perihelion and aphelion is only 3.4% (5.1 million km). Perihelion presently occurs around January 3, while aphelion is around July 4. When the orbit is at its most elliptical, the amount of solar radiation at perihelion will be about 23% greater than at aphelion.

Season (Northern Hemisphere) Durations
data from United States Naval Observatory
Year Date: GMT Season Duration
2005 Winter Solstice 12/21/2005 18:35 88.99 days
2006 Spring Equinox 3/20/2006 18:26 92.75 days
2006 Summer Solstice 6/21/2006 12:26 93.65 days
2006 Autumn Equinox 9/23/2006 4:03 89.85 days
2006 Winter Solstice 12/22/2006 0:22 88.99 days
2007 Spring Equinox 3/21/2007 0:07 92.75 days
2007 Summer Solstice 6/21/2007 18:06 93.66 days
2007 Autumn Equinox 9/23/2007 9:51 89.85 days
2007 Winter Solstice 12/22/2007 06:08
 

Orbital mechanics requires that the length of the seasons be proportional to the areas of the seasonal quadrants, so when the eccentricity is extreme, the seasons on the far side of the orbit can be substantially longer in duration. When autumn and winter occur at closest approach, as is the case currently in the northern hemisphere, the earth is moving at its maximum velocity and therefore autumn and winter are slightly shorter than spring and summer. Thus, summer in the northern hemisphere is 4.66 days longer than winter and spring is 2.9 days longer than autumn.

Axial tilt (obliquity)

Main article: Axial tilt
22.1-24.5° range of Earth's obliquity.

The angle of the Earth's axial tilt (obliquity) varies with respect to the plane of the Earth's orbit. These slow 2.4° obliquity variations are roughly periodic, taking approximately 41,000 years to shift between a tilt of 22.1° and 24.5° and back again. When the obliquity increases, the amplitude of the seasonal cycle in insolation (INcoming SOLar radiATION) increases, with summers in both hemispheres receiving more radiative flux from the Sun, and the winters less radiative flux.

But these changes of opposite sign in the summer and winter are not of the same magnitude. The annual mean insolation increases in high latitudes with increasing obliquity, while lower latitudes experience a reduction in insolation. Cooler summers are suspected of encouraging the start of an ice age by melting less of the previous winter's ice and snow. So can it be argued that lower obliquity favors ice ages both because of the mean insolation reduction in high latitudes as well as the additional reduction in summer insolation. However no significant climate changes are associated with extreme axial tilts.

Scientists using computer models to study more extreme tilts than those that actually occur have concluded that climate extremes at high obliquity would be particularly threatening to advanced forms of life that presently exist on Earth. They noted that high obliquity would not likely sterilize a planet completely, but would make it harder for fragile, warm-blooded land-based life to thrive as it does today.[5]

Currently the Earth is tilted at 23.44 degrees from its orbital plane, roughly half way between its extreme values. The tilt is in the decreasing phase of its cycle, and will reach its minimum value around the year 10,000 C.E.. This trend, by itself, would tend to make winters warmer and summers colder; however increases in greenhouse gases may overpower this effect.


Axial precession

Main article: Axial precession (astronomy)
Precessional movement.

Precession is the change in the direction of the Earth's axis of rotation relative to the fixed stars, with a period of roughly 26,000 years. This gyroscopic motion is due to the tidal forces exerted by the sun and the moon on the solid Earth, associated with the fact that the Earth is an oblate spheroid shape and not a perfect sphere. The sun and moon contribute roughly equally to this effect.

When the axis is aligned so it points toward the Sun during perihelion, one polar hemisphere will have a greater difference between the seasons while the other hemisphere will have milder seasons. The hemisphere which is in summer at perihelion will receive much of the corresponding increase in solar radiation, but that same hemisphere will be in winter at aphelion and have a colder winter. The other hemisphere will have a relatively warmer winter and cooler summer.

When the Earth's axis is aligned such that aphelion and perihelion occur near the equinoxes, the Northern and Southern Hemispheres will have similar contrasts in the seasons.

At present, perihelion occurs during the Southern Hemisphere's summer, and aphelion is reached during the southern winter. Thus the Southern Hemisphere seasons are somewhat more extreme than the Northern Hemisphere seasons, when other factors are equal.


Apsidal precession

Planets orbiting the Sun follow elliptical (oval) orbits that rotate gradually over time (apsidal precession). The eccentricity of this ellipse is exaggerated for visualization. Most orbits in the Solar System have a much smaller eccentricity, making them nearly circular.
Effects of apsidal precession on the seasons

In addition, the orbital ellipse itself precesses in space, primarily as a result of interactions with Jupiter and Saturn. This orbital precession is in the same sense to the gyroscopic motion of the axis of rotation, shortening the period of the precession of the equinoxes with respect to the perihelion from 25,771.5 to ~21,636 years.


Orbital inclination

Main article: Orbital inclination

The inclination of Earth's orbit drifts up and down relative to its present orbit with a cycle having a period of about 70,000 years. Milankovitch did not study this three-dimensional movement. This movement is known as "precession of the ecliptic" or "planetary precession".

More recent researchers noted this drift and that the orbit also moves relative to the orbits of the other planets. The invariable plane, the plane that represents the angular momentum of the solar system, is approximately the orbital plane of Jupiter. The inclination of the Earth's orbit has a 100,000 year cycle relative to the invariable plane; by chance, this is very similar to the 100,000 year eccentricity period. This 100,000-year cycle closely matches the 100,000-year pattern of ice ages.

It has been proposed that a disk of dust and other debris exists in the invariable plane, and this affects the Earth's climate through several possible means. The Earth presently moves through this plane around January 9 and July 9, when there is an increase in radar-detected meteors and meteor-related noctilucent clouds.[6][7]

A study of the chronology of Antarctic ice cores using oxygen to nitrogen ratios in air bubbles trapped in the ice, which appear to respond directly to the local insolation, concluded that the climatic response documented in the ice cores was driven by Northern Hemisphere insolation as proposed by the Milankovitch hypothesis (Kawamura et al., Nature, 23 August 2007, vol 448, p912-917). This is an additional validation of the Milankovitch hypothesis by a relatively novel method, and is inconsistent with the "inclination" theory of the 100,000-year cycle.

Problems

Because the observed periodicities of climate fit so well with the orbital periods, the orbital theory has overwhelming support. Nonetheless, there are several difficulties in reconciling theory with observations.

The nature of sediments can vary in a cyclic fashion, and these cycles can be displayed in the sedimentary record. Here, cycles can be observed in the colouration and resistance of different strata

100,000-year problem

The 100,000-year problem is that the eccentricity variations have a significantly smaller impact on solar forcing than precession or obliquity and hence might be expected to produce the weakest effects. However, observations show that during the last 1 million years, the strongest climate signal is the 100,000-year cycle. In addition, despite the relatively large 100,000-year cycle, some have argued that the length of the climate record is insufficient to establish a statistically significant relationship between climate and eccentricity variations.[8] Some models can however reproduce the 100,000 year cycles as a result of non-linear interactions between small changes in the Earth's orbit and internal oscillations of the climate system.[9][10]

400,000-year problem

The 400,000-year problem is that the eccentricity variations have a strong 400,000-year cycle. That cycle is only clearly present in climate records older than the last million years. If the 100 ka variations are having such a strong effect, the 400 ka variations might also be expected to be apparent. This is also known as the stage 11 problem, after the interglacial in marine isotopic stage 11 which would be unexpected if the 400,000-year cycle has an impact on climate. The relative absence of this periodicity in the marine isotopic record may be due, at least in part, to the response times of the climate system components involved — in particular, the carbon cycle.

Stage 5 problem

The stage 5 problem refers to the timing of the penultimate interglacial (in marine isotopic stage 5) which appears to have begun 10 thousand years in advance of the solar forcing hypothesized to have been causing it. This is also referred to as the causality problem.

Effect exceeds cause

420,000 years of ice core data from Vostok, Antarctica research station.

The effects of these variations are primarily believed to be due to variations in the intensity of solar radiation upon various parts of the globe. Observations show climate behaviour is much more intense than the calculated variations. Various internal characteristics of climate systems are believed to be sensitive to the insolation changes, causing amplification (positive feedback) and damping responses (negative feedback).

The unsplit peak problem

The unsplit peak problem refers to the fact that eccentricity has cleanly resolved variations at both the 95 and 125 ka periods. A sufficiently long, well-dated record of climate change should be able to resolve both frequencies,[11] but some researchers interpret climate records of the last million years as showing only a single spectral peak at 100 ka periodicity. It is debatable whether the quality of existing data ought to be sufficient to resolve both frequencies over the last million years.

The transition problem

Variations of Cyle Times, curves determined from ocean sediments

The transition problem refers to the change in the frequency of climate variations 1 million years ago. From 1-3 million years, climate had a dominant mode matching the 41 ka cycle in obliquity. After 1 million years ago, this changed to a 100 ka variation matching eccentricity. No reason for this change has been established.

Identifying dominant factor

Milankovic himself believed that reductions in summer insolation in northern high latitudes was the dominant factor leading to glaciation, which led to him (incorrectly) deducing an approximately 41 kyr period for ice ages [12]. Subsequent research has shown that the 100 kyr eccentricity cycle is more important, resulting in 100,000-year ice age cycles of the Quaternary glaciation over the last few million years.

Theory incomplete

The Milankovitch theory of climate change is not perfectly worked out; in particular, the largest observed response is at the 100,000-year timescale, but the forcing is apparently small at this scale, in regard to the ice ages.[13] Various explanations for this discrepancy have been proposed, including frequency modulation[14] or various feedbacks (from carbon dioxide, cosmic rays or from ice sheet dynamics).

Present and future conditions

Past and future of daily average insolation at top of the atmosphere on the day of the summer solstice, at 65 N latitude. The green curve is with eccentricity e hypothetically set to 0. The red curve uses the actual (predicted) value of e. Blue dot is current conditions, at 2 ky A.D.

As mentioned above, at present, perihelion occurs during the Southern Hemisphere's summer and aphelion during the southern winter. Thus the Southern Hemisphere seasons should tend to be somewhat more extreme than the Northern Hemisphere seasons. The relatively low eccentricity of the present orbit results in a 6.8% difference in the amount of solar radiation during summer in the two hemispheres.

Since orbital variations are predictable,[15] if one has a model that relates orbital variations to climate, it is possible to run such a model forward to "predict" future climate. Two caveats are necessary: that anthropogenic effects may modify or even overwhelm orbital effects and that the mechanism by which orbital forcing influences climate is not well understood.

The amount of solar radiation (insolation) in the Northern Hemisphere at 65° N seems to be related to occurrence of an ice age. Astronomical calculations show that 65° N summer insolation should increase gradually over the next 25,000 years. A regime of eccentricity lower than the current value will last for about the next 100,000 years. Changes in Northern Hemisphere summer insolation will be dominated by changes in obliquity ε. No declines in 65° N summer insolation, sufficient to cause an ice age, are expected in the next 50,000 years.

An often-cited 1980 study by Imbrie and Imbrie determined that, "Ignoring anthropogenic and other possible sources of variation acting at frequencies higher than one cycle per 19,000 years, this model predicts that the long-term cooling trend which began some 6,000 years ago will continue for the next 23,000 years."[16]

More recent work by Berger and Loutre suggests that the current warm climate may last another 50,000 years.[17]

The best chances for a decline in Northern hemisphere summer insolation that would be sufficient for triggering an ice age is at 130,000 years or possibly as far out at 620,000 years.[18]

See also

References

  1. ↑ Hays, J.D.; Imbrie, J.; Shackleton, N.J. (1976). "Variations in the Earth's Orbit: Pacemaker of the Ice Ages". Science 194 (4270): 1121–1132. doi:10.1126/science.194.4270.1121. PMID 17790893. 
  2. ↑ Girkin, Amy Negich (2005). A Computational Study on the Evolution of the Dynamics of the Obliquity of the Earth. (Master of Science thesis), Miami University.
  3. ↑ Berger A., Loutre M.F., Mélice J.L. (2006). "Equatorial insolation: from precession harmonics to eccentricity frequencies" (PDF). Clim. Past Discuss. 2: 519–533. doi:10.5194/cpd-2-519-2006. http://www.clim-past-discuss.net/2/519/2006/cpd-2-519-2006.pdf. 
  4. ↑ "Deliverables of IEA SHC - Task 26: Solar Combisystems" (PDF). 
  5. ↑ Williams, D.M., Pollard, P. (2002). "Earth-like worlds on eccentric orbits: excursions beyond the habitable zone". Inter. J. Astrobio. 1: 21–9. http://physics.bd.psu.edu/faculty/williams/3DEarthClimate/ija2003.pdf. 
  6. ↑ Richard A Muller, Gordon J MacDonald (1997). "Glacial Cycles and Astronomical Forcing". Science 277 (1997/07/11): 215–8. doi:10.1126/science.277.5323.215. 
  7. ↑ "Origin of the 100 kyr Glacial Cycle: eccentricity or orbital inclination?". Richard A Muller. http://muller.lbl.gov/papers/nature.html. Retrieved March 2, 2005. 
  8. ↑ Wunsch, Carl (2004). "Quantitative estimate of the Milankovitch-forced contribution to observed Quaternary climate change". Quaternary Science Reviews 23: 1001–12. doi:10.1016/j.quascirev.2004.02.014. 
  9. ↑ Ghil, Michael (1994). "Cryothermodynamics: the chaotic dynamics of paleoclimate". Physica D 77 (1-3): 130–159. doi:10.1016/0167-2789(94)90131-7. 
  10. ↑ Gildor H, Tziperman E (2000). "Sea ice as the glacial cycles' climate switch: Role of seasonal and orbital forcing". Paleoceanography 15 (6): 605–615. doi:10.1029/1999PA000461. 
  11. ↑ Zachos JC, Shackleton NJ, Revenaugh JS, Pälike H, Flower BP (April 2001). "Climate response to orbital forcing across the Oligocene-Miocene boundary". Science 292 (5515): 274–8. doi:10.1126/science.1058288. PMID 11303100. http://www.sciencemag.org/cgi/pmidlookup?view=long&pmid=11303100. 
  12. ↑ Imbrie and Imbrie; Ice Ages, solving the mystery, p 158
  13. ↑ Milankovitch, Milutin (1998) [1941]. Canon of Insolation and the Ice Age Problem. Belgrade: Zavod za Udz̆benike i Nastavna Sredstva. ISBN 8617066199. ; see also "Astronomical Theory of Climate Change". http://www.ncdc.noaa.gov/paleo/milankovitch.html. 
  14. ↑ http://www.geolab.unc.edu/faculty/rial/GPCRial2.pdf
  15. ↑ F. Varadi, B. Runnegar, M. Ghil (2003). "Successive Refinements in Long-Term Integrations of Planetary Orbits" (PDF). The Astrophysical Journal 592: 620–630. doi:10.1086/375560. http://astrobiology.ucla.edu/OTHER/SSO/SolarSysInt.pdf. 
  16. ↑ J Imbrie, J Z Imbrie (1980). "Modeling the Climatic Response to Orbital Variations". Science 207 (1980/02/29): 943–953. doi:10.1126/science.207.4434.943. PMID 17830447. 
  17. ↑ Berger A, Loutre MF (2002). "Climate: An exceptionally long interglacial ahead?". Science 297 (5585): 1287–8. doi:10.1126/science.1076120. PMID 12193773. 
  18. ↑ http://amper.ped.muni.cz/gw/articles/html.format/orb_forc.html

Further reading

  • Roe G (2006). "In defense of Milankovitch". Geophysical Research Letters 33: L24703. doi:10.1029/2006GL027817.  This shows that Milankovitch theory fits the data extremely well, over the past million years, provided that we consider derivatives.
  • Zachos J, Pagani M, Sloan L, Thomas E, Billups K (2001). "Trends, Rhythms, and Aberrations in Global Climate 65 Ma to Present". Science 292 (5517): 686–693. doi:10.1126/science.1059412. PMID 11326091. 
    This review article discusses cycles and large-scale changes in the global climate during the Cenozoic Era.

External links